第05章 功能性测试
第05章 功能性测试
一、概述
功能性测试包括如下三种测试:
- 边界值测试
- 等价类测试
- 基于决策表的测试
这三类都是黑盒测试,不需要看源代码,只需要看输入、输出、从功能开始分析。会把功能分为一个一个用例来测试,并且补充用例说明,有完整的输入、输出信息,用来评判输出的正确性。不同的测试方法有优点也有缺点。
二、边界测试
对于函数$Y=f(x_1,x_2)$,要求$a\leq x_1 \leq b$,$c\leq x_2 \leq d$, 边界值测试的取值:最小值、略高于最小值、正常值、略高于最高值、最高值。因为边界测试在定义的时候就是基于单缺陷假设。
1)单缺陷假设
单缺陷假设:失效很少情况是由两个或者更多的缺陷同时引起的,大多数情况只是一个因素引起。公式:$N$个变量的测试用例的数量:$4N+1$
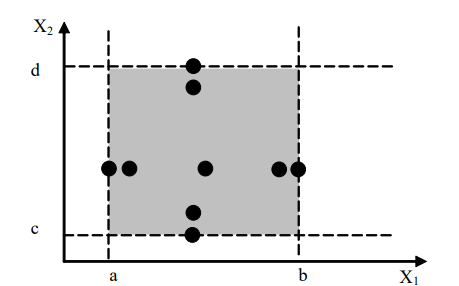
2)健壮性测试
健壮性测试:除了五个边界值,我们再增加一个略小于最小值、一个略大于最大值(即要考虑无效值输入)
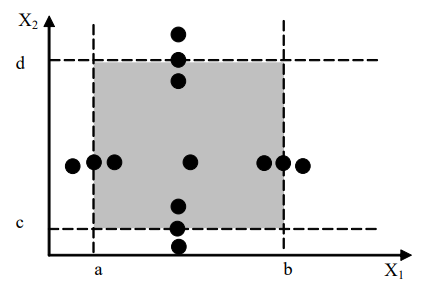
公式:N个变量的测试用例的数量:$6N+1$
3)最坏情况
最坏情况测试:拒绝单缺陷假设, 考虑全部边界输入的组合。N个变量的测试用例:$5^N$(每个变量都要考虑:最小值、略高于最小值、正常值、略高于最高值、最高值,也就是每个变量都是五个情况)加入
- 假如还要考虑健壮性,需要考虑无效数据的输入,那就需要$7^N$的输入。
- 例如:三角形问题边界值测试,abc三个变量,一般法$4\times 3 + 1=13$,最坏情况$5^3=125$个
4)随机测试
随机测试:即便完成所有边界值测试,还可以用随机测试,用随机函数取出测试值,但是需要考虑随机生成的数据量
三、等价类测试
划分:互不相交的一组子集,这些子集的并集是全集。
1)弱(单缺陷)一般等价类
- 对于函数$Y=f(x_1,x_2)$,
- $a\leq x_1 \leq d$,等价区间:$[a,b), [b,c), [c,d], N=3$
- $e\leq x_2 \leq g$,等价区间:$[e,f), [f,g],M=3$
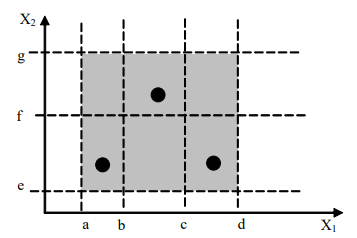
- 考虑单缺陷假设覆盖,测试数为:$max(N,M)$中的最大者
- 考虑多缺陷假设覆盖,测试的数量:$N\times M$
- 假如我们在分类的时候,可以发现有很明显的分类划分(典型的就是三角形例子,比如等腰三角形、等边三角形、非等边三角形、非三角形)
2)强(多缺陷)一般等价类
- 测试数量$M\times N$,考虑不同划分的笛卡尔积
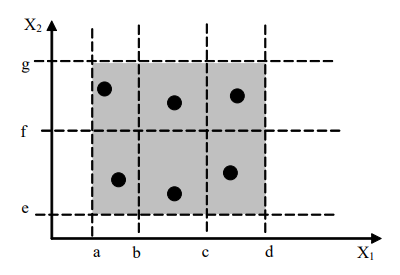
3)弱健壮等价类测试
- 弱(单缺陷)健壮(考虑无效值)
- 测试数量:$max(N,M) + 2$(2是变量的个数)
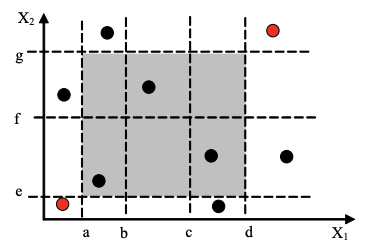
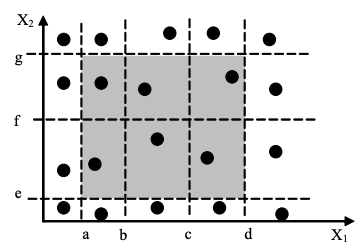
4)强健壮等价类测试
- 强:多缺陷组合(笛卡尔积)
- 健壮:考虑无效值
- 所有的区域全部覆盖:$(M+2)\times (N+2)$
5)总结
- 两种软件缺陷特征假设:单缺陷假设(弱)多缺陷假设(强)
- 考虑无效输入:健壮性
- 最坏情况:基于多缺陷假设
四、决策表的测试
决策表适用的软件的类型是什么?有比较复杂的一个逻辑关系,它的业务流很复杂,需要有很多的一些判断的一些这个场景,有不同的一些输入输出的这种逻辑关系,这种情况下的话,我们只用这种边界值也好,等价类很难达到一个比较好的测试效果。
决策表有四个部分,桩部分、条目部分、条件部分、行动部分
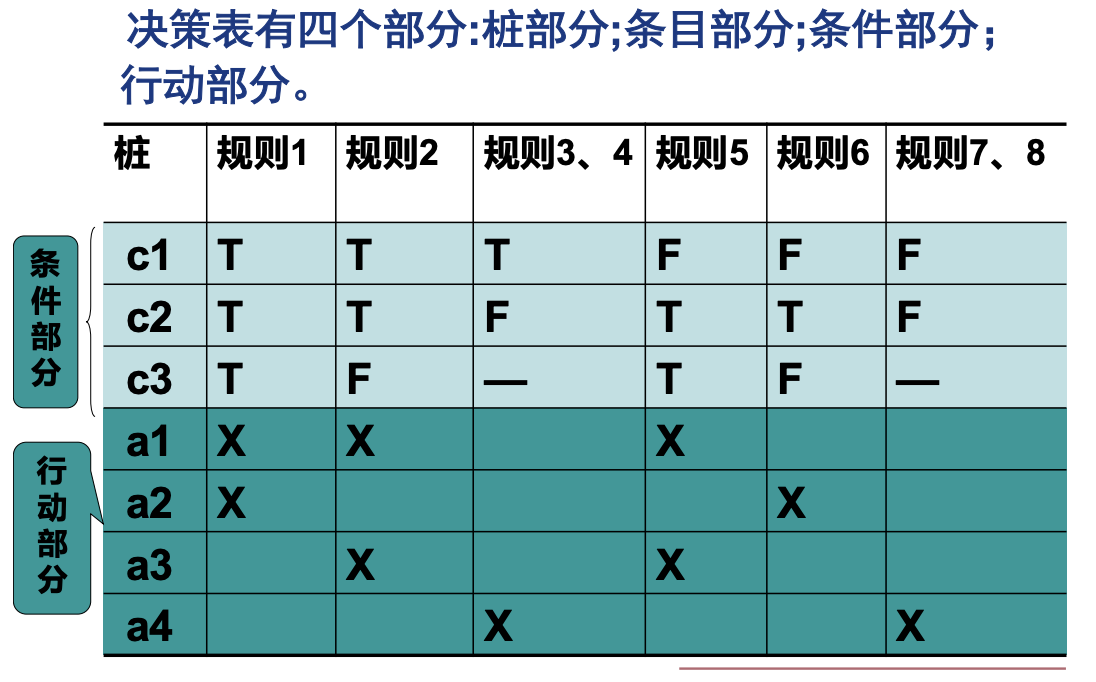
具体例子:
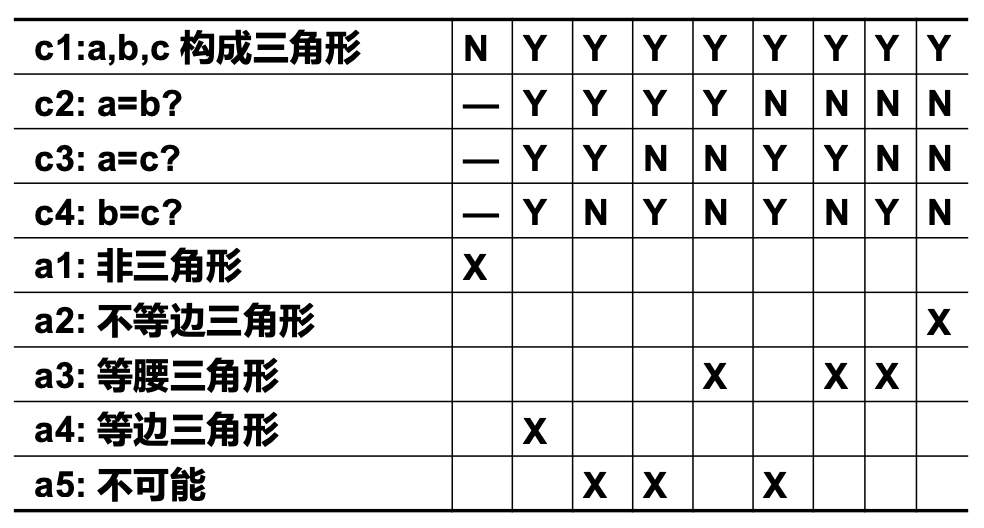
五、测试效率
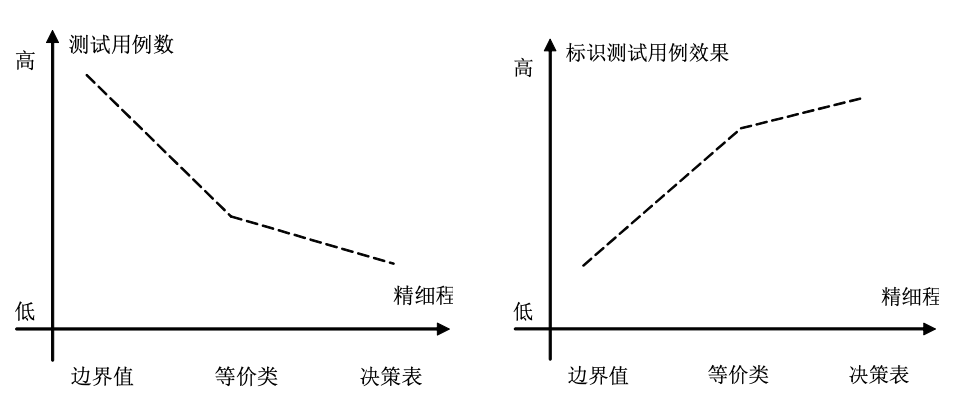
六、测试的选择
- 如果变量引用物理量,采用边界值分析和等价类测试
- 如果变量是独立,采用边界值分析和等价类测试
- 如果变量不是独立的,采用决策表测试
- 如果可以保证单缺陷假设,采用边界值分析和健壮性测试
- 如果可以保证多缺陷假设,采用最坏情况测试,健壮性最坏情况测试、决策表测试
- 如果程序包含大量例外处理,采用健壮性测试和决策表测试
- 如果变量引用的是逻辑量,采用等价类测试和决策表测试